Trochę historii 'dziel i zwyciężaj’
Maksyma „dziel i zwyciężaj” (ang. divide and conquer) powinna kojarzyć Ci się ze starożytnym Rzymem, gdzie główne sukcesy militarne tego Państwa, szły razem z znakomitą dyplomacją. Rzymianie, gdy tylko mogli, koncentrowali się na walce z jednym przeciwnikiem, szukając jak największej liczby sojuszników (z reguły tymczasowych), którzy mogli przyłączyć się do walki z wrogiem. Nie przeszkadzało im to jednak spiskować za plecami swoich sojuszników w taki sam sposób.
Idea tego algorytmu jest podobna. Wyobraź sobie, że masz olbrzymią, zawierającą miliony elementów, tablicę. Tablica ta zawiera losowo przydzielone liczby. W tym olbrzymim ciągu chciałbyś znaleźć najmniejszą występującą wartość. Najprostszym rozwiązaniem tego problemu byłoby po prostu przejrzenie tej tablicy, indeks po indeksie, i wypisywanie numeru pod którym kryje się najmniejsza cyfra, po czym porównanie go z sąsiadem i skreślanie tego który jest większy. W końcu po ostatnim porównanie otrzymałbyś wynik. Jednak jakbyś miał to robić sam, zajęłoby Ci to bardzo dużo czasu. A co jeśli tą pracą podzieliłbyś się z kolegami? Każdy z was mógłby przejrzeć mały kawałek ciągu, a na końcu porównywalibyście już jedynie wartości między kandydatami z każdego podciągu. Tak samo możesz zrobić to używając komputera.
Spójrz na naiwną implementację algorytmu typu 'dziel i zwyciężaj’:
public class MinValue {
public static void main(String[] args) {
int [] prices = {20,15,103,15,165,4,91,56,82,98};
System.out.println(searchMinimum(prices));
}
private static int searchMinimum(int [] prices) {
int mininiumValue = prices[0];
for (int i = 1; i < prices.length; i++) {
if (prices[i] < mininiumValue) {
mininiumValue = prices[i];
}
}
return mininiumValue;
}
}
Faktycznie wynik jest właściwy i wynosi: 4.
Szukanie minimum
Przeszukiwanie działa w bardzo prymitywny sposób. Program porównuje kolejne liczby zapisane w tablicy ze sobą. I w przypadku, gdy jedna jest mniejsza od drugiej, przypisuje tymczasowej ją do zmiennej minimumValue. Końcowa wartość jest wyświetlana na konsolę.
Jak się domyślasz nie jest to najszybszy sposób, aby rozwiązać ten problem. Na pewno jest on najprostszy do implementacji i najłatwiejszy do zrozumienia. O ile porównanie dziesięciu liczb ze sobą dla współczesnego przeciętnej klasy komputera nie dzieje się w ułamku sekundy, o tyle ten sam algorytm przy przeglądaniu milionów rekordów, może wykonywać się bardzo długo. Dlatego musisz być sprytniejszy i spróbować podzielić sobie pracę np. na kilka kawałków, zamiast przeglądać wszystkie wartości po kolei.
Na pomoc przychodzi algorytm 'dziel i zwyciężaj’.
public class DivideAndConquerAlgorithm {
private static int[] prices = { 20, 15, 103, 15, 165, 4, 91, 56, 82, 98 };
private static int minimumValue = Integer.MAX_VALUE;
public static void main(String[] args) {
System.out.println(searchMinimum(prices));
}
private static int searchMinimum(int[] prices) {
return divideAndConquer(0, prices.length - 1);
}
private static int divideAndConquer(int left, int right) {
if (left == right) {
minimumValue = prices[left];
} else {
if (left == right - 1) {
if (prices[left] < prices[right]) {
minimumValue = prices[left];
} else {
minimumValue = prices[right];
}
} else {
int middle = (left + right) / 2;
divideAndConquer(left, middle);
int temporaryMinimum = minimumValue;
divideAndConquer(middle + 1, right);
if (minimumValue > temporaryMinimum) {
minimumValue = temporaryMinimum;
}
}
}
return minimumValue;
}
}
Podział na części
Nowy algorytm korzysta z indeksów zarówno z lewej (od początku) jak i z prawej (na końcu) strony. To ważna zmiana, bowiem nie wymaga już porównywania każdego elementu z sąsiadem. Teraz rekurencyjnie dzielimy tablicę na tyle „małych tablic” ile potrzeba do wykonania obliczeń. Rekurencja jak zawsze działa trochę „od tyłu”, także najpierw sprawdzany jest warunek stopu:
if (left == right) {
minimumValue = prices[left];
Gdy lewy indeks równa się prawemu, oznacza to, że nie ma już więcej wartości do porównywania i zwracana jest ostatnia porównana wartość. Następnie w warunku else wpierw dokonywane jest sprawdzenie, który z dwóch bieżących elementów jest większy:
if (left == right - 1) {
if (prices[left] < prices[right]) {
minimumValue = prices[left];
} else {
minimumValue = prices[right];
}
}
Jeśli lewy indeks wciąż nie znajduje się obok prawej (pamiętaj, że idziemy po elementach od początku i od końca równocześnie). Nie możemy dokonać sprawdzenia, który jest mniejszy. W takim razie należy podzielić tablicę na pół.
else {
int middle = (left + right) / 2;
divideAndConquer(left, middle);
int temporaryMinimum = minimumValue;
divideAndConquer(middle + 1, right);
if (minimumValue > temporaryMinimum) {
minimumValue = temporaryMinimum;
}
}
Podsumownie
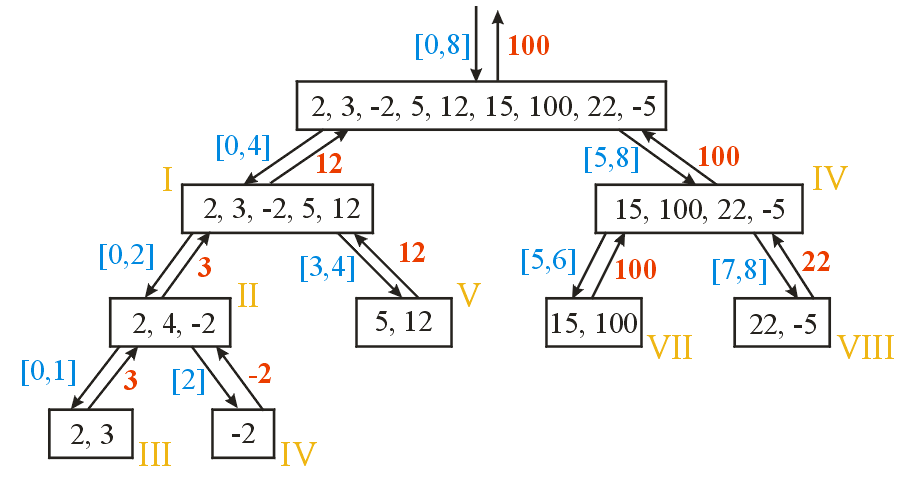
Jednak to nie koniec podziału. Będzie się on odbywał aż tablica nie podzieli się na same małe dwuelementowe tablice, składające się z sąsiadujących elementów. Dopiero w momencie jak lewa część spotka się z prawą dokonywane jest sprawdzenie, który element jest większy i zawracany jest wynik. Świetnym sposobem zobrazowania, jak działa ten algorytm będzie poniższy rysunek.
Co prawda, jest to algorytm sortowania przez podział (merge sort), ale idea jest bardzo podobna.
Jak widzisz zarówno rekurencja i jak algorytmy z rodziny 'dziel i zwyciężaj’ są powszechne używane. Na szczęście większość z nich jest już dawno zaimplementowanych w Javie i nie musisz znać ich wszystkich na pamięć (jednak zawsze warto rozumieć zasadę ich działania). W kolejnym wpisie postaram się przybliżyć Ci działanie algorytmów sortowania.
Polecam także lekcję o sortowaniu: https://developeronthego.pl/algorytmy-dla-poczatkujacych-3-sortowanie/